I thought I'd upload some of my University work, since I'm quite proud of it, so if you want to know about parallel programming, Physics simulations and Nvidia's CUDA then take a read of this http://chriswarbo.webs.com/CUDAProject.pdf
If you're interested in the world of the tiny, and what you can build given some pieces of DNA, take a look here http://chriswarbo.webs.com/DNAEssay.pdf
Showing posts with label physics 4TW. Show all posts
Showing posts with label physics 4TW. Show all posts
Friday, 21 May 2010
Friday, 26 March 2010
Divergence and reduction with complex numbers
I came across this introduction to the concept of "imaginary" numbers, and thought it would be worthwhile to write a post about how cool complex and imaginary numbers actually are.
If you don't know what an imaginary number or a complex number is then don't worry. That link provides quite a nice intro, and I'll give my own here:
An "imaginary" number is a number which doesn't fit anywhere on the number line. No matter how closely you zoom in, or how far along you go, you'll never find it. That's why they're called "imaginary", even though it is an unfortunate name as the other blog points out. Before you dismiss imaginary numbers as useless, let's consider another set of numbers which is made up and doesn't exist in the real world: negative numbers.
Negative numbers cannot exist like the natural (positive) numbers do. You cannot have -5 apples. Nevertheless, negative numbers are useful for made up mathematical worlds, like banking for example, which can have a definite impact on the real, physical world. Negative numbers also arise in situations involving symmetry, relative values and arbitraryness. Let's take a realistic example: if we think of positions, there is no set of coordinate axes in the physical world, and the whole Universe is symmetric spatially, so we can just make up the numbers we use to be anything we find convenient. Let's say we've got a chocolate bar:
We'd like to be able to refer to each section of chocolate in a unique way, so we can say that the bottom left section is at position (0,0), and define our unit of length to be one chocolate section. Thus we can say "The sections at (0,2) and (0,3) have been bitten". Now let's say that Dr Ed Daw has had a busy day and didn't have chance to grab some food. He's so hungry that he doesn't have enough energy to move more than one unit of distance to get the food he needs, but he spies our chocolate bar. Can Dr Daw get the food he needs?:
To find the distance between the doctor and the chocolate we need to know the doctor's position. We can't use a positive number to define the position, since even though there are an infinite number of them, they get less and less accurate the further we look. Instead we have to use a negative number, allowing us to say that Dr Ed Daw is at position (0, -1). We know there is chocolate at (0,0), so to get from his position to the food only takes one unit of distance, since (0,-1)+(0,1)=(0,0). The only reason we had to use a negative number here is because of the way we defined our mathematical model of the situation. There's no such thing as "negative position", but when we used the doctor's negative position to find the distance he has to move, which is a physical quantity, the negative numbers disappeared and we got a meaningful, and correct, answer.
So let's move on to imaginary numbers: Close to the surface of the Earth, gravity is pretty constant, with a value of 9.81 metres per second per second. This means that vertical speed (metres per second, miles per hour, etc.) will go down by 9.81 metres per second (if it's pointing up), or up by 9.81 metres per second (if it's pointing down) every second. Speed describes how your position changes in time (eg. how many metres you move in a second), so the position of something flying through the air will change by the speed which itself will change due to gravity, so the position will curve. The shapes made by these curves are called parabolas and behave like the quantity -Ax^2 + Bx + C, where x is your horizontal position (or you could use time here instead) and A, B and C are numbers specific to what you're looking at. We get a minus sign for the x^2 because gravity points down and we define up to be positive. If we want to know at what position or time a ballistic (falling) object will reach a certain height, what we're really asking is at what position or time does Ax^2 + Bx + C equal the height we're interested in. We can do this with an example: Dr Daw has finished his chocolate and is trying to show off some lasers to his younger, more tanned brother. They each attach a laser to their head, Ed takes the red one and his brother De takes the green one. The lasers need to be kept cool, so they go to the Sheffield Ski Village. While they watch the skiers go past, De asks his brother "When do the skiers get higher than the lasers attached to our heads?". How can Ed work this out, given that the skiers motion can be described by -x^2 + 0x + 5, that De's green laser is a height of 4 and that Ed's red laser is at a height of 6?
Ed knows that he can take the skiers's motion and, using the apex of the jump as position 0, work our at which positions they get above the lasers by saying -x^2 + 5 = 4 when they get above De's laser and -x^2 + 5 = 6 when they cross his laser. Working out the first gives the valid positions, x, as:
-x^2 + 5 = 4
-x^2 = 4 - 5
-x^2 = -1
x^2 = 1
x = +1 or -1
He tells his brother that the skiers will cross the green laser at positions -1 and +1, since they satisfy the equation of motion. He then tries to work out when they cross the red laser:
-x^2 + 5 = 6
-x^2 = 6 - 5
-x^2 = 1
x^2 = -1
Then Ed gets stuck, since there's no positive or negative number he can think of which would fit as x here. Thus he declares to De "There are no solutions, so the skiers never get above my laser.". De is not satisfied with this. He says "That's cheating. I want you to finish working it out.". Ed knows how stubborn his brother is, since he carried on wearing fake tan even after going on "Snog, Marry, Avoid" the previous year, so he invents a number to satisft this equation:
"The skiers cross my laser whenever they get to a position which I will call N. They will also cross the laser if they get to a position -N. Thus, +N and -N are the solutions to this equation."
De is still not satisfied, so he asks his brother what N is. The doctor then explains imaginary numbers to the younger man:
"N is a quantity that is not a positive number, or a negative number, however it is a very useful quantity, since it lets us solve the equation for my laser. You can't find it no matter how closely you look between the numbers, or how far along you go. This means that its value is orthogonal to the real numbers, since the two are independent, in the same way that you can't change an x coordinate by moving in the y direction. In fact, we could draw a diagram using the real numbers as an x axis and these imaginary ones as the y axis."
"I'm confused." said De, "Will you please draw me such a diagram?"
"I can't be arsed," Ed replied, "so here's one I found on Wikipedia."
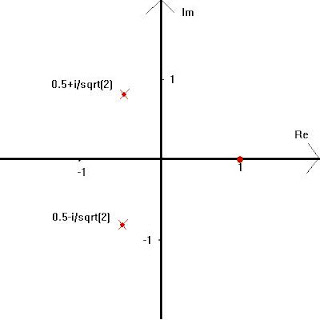Using this diagram, Ed could explain to his brother how a Real number (Re) sits on the horizontal line, how an Imaginary number (Im) sits on the vertical line, and how the quadrants are filled with numbers that have an imaginary part and a real part, and are called Complex numbers. De seemed to understand, but had some questions:
"OK, I'll accept what you just said, but then where does our quantity N fit in this diagram? Also, there are some undefined variables; what is the value of the "i" that's written on the diagram?"
"The "i" represents the Imaginary unit." Ed explained, "It's equivalent to the number 1 for natural numbers, and -1 for negative numbers. Every Imaginary number is made out of some quantity of i."
"So what is the value of i?"
"The imaginary unit is defined by the equation i^2 = -1. No more, no less."
"But that's the equation for the skiers crossing your laser! That means that N = i and the skiers will cross if they ever get to a position i, which they can never do because imaginary space is orthogonal to physical space, so no force can ever push them off the Real lines for x, y and z."
"Well done" said an impressed Ed "but you're forgetting how to do square roots! There are always two square roots of a number, just like we had +N and -N. That means that i^2 = -1 and (-i)^2 = -1. So tell me, does N = i or does N = -i?"
De thought about this for a minute before declaring "There's no way of telling! If N = i then N^2 = -1 since i^2 = -1, but also (-N)^2 = -1 since the minus signs cancel so -N = i. But also, (-i)^2 = -1 so N = -i and, because the minus signs cancel, i^2 = -1, so N = i. So N = +i or -i and -N = +i or -i, they're equal!"
"Don't be too hasty to call them equal!" cautioned Ed "If N = -N then i = -i and I could do the following:
i = -i This is what you are claiming
i + i = -i + i We can add i to each side to preserve the equality
2i = 0 Adding i to i gives 2i, whilst adding i to -i gives zero
i = 0 We can divide both sides by 2 and preserve the equality
i*i = 0*i We can multiply each side by i and preserve the equality
i*i = 0*0 We showed that i=0 so use that on the right hand side
i*i = 0 We know 0*0=0
-1 = 0 From the definition of i, i*i = -1
We have reached an absurdity! The only conclusion is that i cannot be equal to -i, and thus N cannot be equal to -N."
"So which way around are they?" implored De.
"It's unknowable." replied Ed, "You can use either i = N or i = -N and you'll get the same results. Swapping every i for a -i in any Maths will change nothing, as long as you're consistent in which value (i or -i) you take to be positive. By convention we say that i is positive, and that -i is negative, but that's just a sentence in this silly human language of ours. It has no mathematical meaning, since they are both the imaginary unit, whilst also being distinct and not equal."
"Fascinating!" exclaimed De, "Can you give me some examples of swapping i and -i?"
"No." said Ed stubbornly, "We've taken this example far too off course, so we'll leave Chris to explain that. Now let's take these lasers back to the Hicks before Professor Fox realises we've taken them!"
Q.E.D.
So, why is having two imaginary roots cool? Well, just as in the case of negative numbers, where the physical quantities like length always end up positive despite our use of negative numbers in our made up mathematical models, similarly every physical quantity calculated using imaginary numbers turns out to be real, and furthermore it turns out the same no matter whether you use i as your basic unit of imaginaryness or -i. They both represent the same unknowable pair of imaginary quantities that Ed called +N and -N, and since we can never know the "N"s we may as well use the "i"s, and just treat them as algebraic names (like we would "x" or "p" or any other variable name), and always keep in mind that the equation i^2 = -1 is simultaneous to everything we do.
So on to some examples of swapping the signs. Mathematically, swapping the sign of the "i"s in a number is called "taking the complex conjugate", so Ed's explanation tells us that if we take the complex conjugate of the entirety of Maths, we'll get the same thing that we started with.
In Quantum Mechanics there are imaginary and complex numbers all over the place. Instead of describing things in 3D space with x, y and z being the units of length in each direction, we instead use what is called a Hilbert space, which allows us to use all manner of crazy things as our axes, and any number of them we want. In a complex Hilbert space, ie. a space where positions may include imaginary components, there is what's called a dual space, containing the complex conjugate of everything in the original space. Since taking the complex conjugate doesn't do anything as long as we do it consistently (ie. to everything) then any Hilbert space can be swapped with its dual and nothing about the Maths will change!
A closely related example is that when using Dirac's notation for Quantum Mechanics, we have a "bra" and a "ket" which together make a "braket". 'Bra A' looks like <A|, 'ket A' looks like |A> and a braket looks like <A|A>. The bras represent complex conjugates whilst the kets represent the original values, so <A| is the complex conjugate of |A>. Essentially bras and kets represent views into the Hilbert space and its dual: |A> is A as seen in the Hilbert space we're using, whilst <A| is A as seen in the dual space. Since we can swap the Hilbert space and dual space, we can use bras instead of kets and kets instead of bras and get the same answers to our calculations.
Another interesting use of complex conjugates is in the transactional interpretation of Quantum Mechanics. Quantum Mechanics involves lots of funky Maths, which works, but when people look for stories they can tell about what the Maths is doing (for example, if BBC's Horizon wants a voice-over to an irrelevant analogy) then there are several ways of explaining it. A nice idea is the transactional interpretation, where Schroedinger's equation (which describes how a quantum system changes over time) and its complex conjugate (which arises due to relativity) are both taken to be actual Physical laws. In other interpretations, the complex conjugate form is discarded as unphysical (like Ed tried to initially do with the red laser equation), leaving the Schroedinger equation to describe the movement of waves over time. This is a bit of a rubbish thing to do though, since we know that our imaginary units represent the same quantities, so we'd like a solution which doesn't involve throwing away whichever imaginary 'direction' is inconvenient. If we do keep the complex conjugate version then we get a second equation describing the movement of waves backwards in time, which is pretty peculiar but we're just upright apes so that's no reason to stop investigating.
The transactional interpretation of Quantum Mechanics shows that every event sends waves forwards and backwards in time, for example the emmission or absorbtion of radiation. However, we don't see these "waves from the future" since they stack up on top of each other and end up cancelling each other out. For example, an electron emits radiation and sends it forwards and backwards in time. Later on an electron absorbs this radiation and it too sends waves forwards and backwards in time. The forwards-in-time wave given out by the absorbtion exactly cancels with the forward-in-time wave given out by the emission, so at times after the absorbtion, the waves cancel to nothing. Likewise the backwards-in-time waves cancel for all times before the emmission, so there's nothing about an event which exists before it occurs (since the waves, when multiplied by their ocmplex conjugate, give probabilities. If the waves cancel to zero then the probability of anything to do with the wave existing at that point is zero). In the time between emmission and absorbtion, there is a wave travelling forwards in time and a wave travelling backwards in time, which turn out not to cancel, and we see one wave (the sum of the two) as we travel along in time. This is nice since we can swap the "i"s for "-i"s and get the same results, we'd just change the direction in time we're travelling in from "forwards" to "backwards", but like the +N and -N of Ed Daw's example, we've just made up those concepts as if they mean something. The reality is that there's no way of making such a distinction, so it becomes meaningless to try and find the values of "+N", "-N", "forwards" or "backwards". Just choose one and stick to it, like we normally choose "i" to be the positive root and "forward" to be the direction we perceive as our neurons interact thermodynamically.
If you don't know what an imaginary number or a complex number is then don't worry. That link provides quite a nice intro, and I'll give my own here:
An "imaginary" number is a number which doesn't fit anywhere on the number line. No matter how closely you zoom in, or how far along you go, you'll never find it. That's why they're called "imaginary", even though it is an unfortunate name as the other blog points out. Before you dismiss imaginary numbers as useless, let's consider another set of numbers which is made up and doesn't exist in the real world: negative numbers.
Negative numbers cannot exist like the natural (positive) numbers do. You cannot have -5 apples. Nevertheless, negative numbers are useful for made up mathematical worlds, like banking for example, which can have a definite impact on the real, physical world. Negative numbers also arise in situations involving symmetry, relative values and arbitraryness. Let's take a realistic example: if we think of positions, there is no set of coordinate axes in the physical world, and the whole Universe is symmetric spatially, so we can just make up the numbers we use to be anything we find convenient. Let's say we've got a chocolate bar:
We'd like to be able to refer to each section of chocolate in a unique way, so we can say that the bottom left section is at position (0,0), and define our unit of length to be one chocolate section. Thus we can say "The sections at (0,2) and (0,3) have been bitten". Now let's say that Dr Ed Daw has had a busy day and didn't have chance to grab some food. He's so hungry that he doesn't have enough energy to move more than one unit of distance to get the food he needs, but he spies our chocolate bar. Can Dr Daw get the food he needs?:
To find the distance between the doctor and the chocolate we need to know the doctor's position. We can't use a positive number to define the position, since even though there are an infinite number of them, they get less and less accurate the further we look. Instead we have to use a negative number, allowing us to say that Dr Ed Daw is at position (0, -1). We know there is chocolate at (0,0), so to get from his position to the food only takes one unit of distance, since (0,-1)+(0,1)=(0,0). The only reason we had to use a negative number here is because of the way we defined our mathematical model of the situation. There's no such thing as "negative position", but when we used the doctor's negative position to find the distance he has to move, which is a physical quantity, the negative numbers disappeared and we got a meaningful, and correct, answer.So let's move on to imaginary numbers: Close to the surface of the Earth, gravity is pretty constant, with a value of 9.81 metres per second per second. This means that vertical speed (metres per second, miles per hour, etc.) will go down by 9.81 metres per second (if it's pointing up), or up by 9.81 metres per second (if it's pointing down) every second. Speed describes how your position changes in time (eg. how many metres you move in a second), so the position of something flying through the air will change by the speed which itself will change due to gravity, so the position will curve. The shapes made by these curves are called parabolas and behave like the quantity -Ax^2 + Bx + C, where x is your horizontal position (or you could use time here instead) and A, B and C are numbers specific to what you're looking at. We get a minus sign for the x^2 because gravity points down and we define up to be positive. If we want to know at what position or time a ballistic (falling) object will reach a certain height, what we're really asking is at what position or time does Ax^2 + Bx + C equal the height we're interested in. We can do this with an example: Dr Daw has finished his chocolate and is trying to show off some lasers to his younger, more tanned brother. They each attach a laser to their head, Ed takes the red one and his brother De takes the green one. The lasers need to be kept cool, so they go to the Sheffield Ski Village. While they watch the skiers go past, De asks his brother "When do the skiers get higher than the lasers attached to our heads?". How can Ed work this out, given that the skiers motion can be described by -x^2 + 0x + 5, that De's green laser is a height of 4 and that Ed's red laser is at a height of 6?
Ed knows that he can take the skiers's motion and, using the apex of the jump as position 0, work our at which positions they get above the lasers by saying -x^2 + 5 = 4 when they get above De's laser and -x^2 + 5 = 6 when they cross his laser. Working out the first gives the valid positions, x, as:-x^2 + 5 = 4
-x^2 = 4 - 5
-x^2 = -1
x^2 = 1
x = +1 or -1
He tells his brother that the skiers will cross the green laser at positions -1 and +1, since they satisfy the equation of motion. He then tries to work out when they cross the red laser:
-x^2 + 5 = 6
-x^2 = 6 - 5
-x^2 = 1
x^2 = -1
Then Ed gets stuck, since there's no positive or negative number he can think of which would fit as x here. Thus he declares to De "There are no solutions, so the skiers never get above my laser.". De is not satisfied with this. He says "That's cheating. I want you to finish working it out.". Ed knows how stubborn his brother is, since he carried on wearing fake tan even after going on "Snog, Marry, Avoid" the previous year, so he invents a number to satisft this equation:
"The skiers cross my laser whenever they get to a position which I will call N. They will also cross the laser if they get to a position -N. Thus, +N and -N are the solutions to this equation."
De is still not satisfied, so he asks his brother what N is. The doctor then explains imaginary numbers to the younger man:
"N is a quantity that is not a positive number, or a negative number, however it is a very useful quantity, since it lets us solve the equation for my laser. You can't find it no matter how closely you look between the numbers, or how far along you go. This means that its value is orthogonal to the real numbers, since the two are independent, in the same way that you can't change an x coordinate by moving in the y direction. In fact, we could draw a diagram using the real numbers as an x axis and these imaginary ones as the y axis."
"I'm confused." said De, "Will you please draw me such a diagram?"
"I can't be arsed," Ed replied, "so here's one I found on Wikipedia."
Using this diagram, Ed could explain to his brother how a Real number (Re) sits on the horizontal line, how an Imaginary number (Im) sits on the vertical line, and how the quadrants are filled with numbers that have an imaginary part and a real part, and are called Complex numbers. De seemed to understand, but had some questions:"OK, I'll accept what you just said, but then where does our quantity N fit in this diagram? Also, there are some undefined variables; what is the value of the "i" that's written on the diagram?"
"The "i" represents the Imaginary unit." Ed explained, "It's equivalent to the number 1 for natural numbers, and -1 for negative numbers. Every Imaginary number is made out of some quantity of i."
"So what is the value of i?"
"The imaginary unit is defined by the equation i^2 = -1. No more, no less."
"But that's the equation for the skiers crossing your laser! That means that N = i and the skiers will cross if they ever get to a position i, which they can never do because imaginary space is orthogonal to physical space, so no force can ever push them off the Real lines for x, y and z."
"Well done" said an impressed Ed "but you're forgetting how to do square roots! There are always two square roots of a number, just like we had +N and -N. That means that i^2 = -1 and (-i)^2 = -1. So tell me, does N = i or does N = -i?"
De thought about this for a minute before declaring "There's no way of telling! If N = i then N^2 = -1 since i^2 = -1, but also (-N)^2 = -1 since the minus signs cancel so -N = i. But also, (-i)^2 = -1 so N = -i and, because the minus signs cancel, i^2 = -1, so N = i. So N = +i or -i and -N = +i or -i, they're equal!"
"Don't be too hasty to call them equal!" cautioned Ed "If N = -N then i = -i and I could do the following:
i = -i This is what you are claiming
i + i = -i + i We can add i to each side to preserve the equality
2i = 0 Adding i to i gives 2i, whilst adding i to -i gives zero
i = 0 We can divide both sides by 2 and preserve the equality
i*i = 0*i We can multiply each side by i and preserve the equality
i*i = 0*0 We showed that i=0 so use that on the right hand side
i*i = 0 We know 0*0=0
-1 = 0 From the definition of i, i*i = -1
We have reached an absurdity! The only conclusion is that i cannot be equal to -i, and thus N cannot be equal to -N."
"So which way around are they?" implored De.
"It's unknowable." replied Ed, "You can use either i = N or i = -N and you'll get the same results. Swapping every i for a -i in any Maths will change nothing, as long as you're consistent in which value (i or -i) you take to be positive. By convention we say that i is positive, and that -i is negative, but that's just a sentence in this silly human language of ours. It has no mathematical meaning, since they are both the imaginary unit, whilst also being distinct and not equal."
"Fascinating!" exclaimed De, "Can you give me some examples of swapping i and -i?"
"No." said Ed stubbornly, "We've taken this example far too off course, so we'll leave Chris to explain that. Now let's take these lasers back to the Hicks before Professor Fox realises we've taken them!"
Q.E.D.
So, why is having two imaginary roots cool? Well, just as in the case of negative numbers, where the physical quantities like length always end up positive despite our use of negative numbers in our made up mathematical models, similarly every physical quantity calculated using imaginary numbers turns out to be real, and furthermore it turns out the same no matter whether you use i as your basic unit of imaginaryness or -i. They both represent the same unknowable pair of imaginary quantities that Ed called +N and -N, and since we can never know the "N"s we may as well use the "i"s, and just treat them as algebraic names (like we would "x" or "p" or any other variable name), and always keep in mind that the equation i^2 = -1 is simultaneous to everything we do.
So on to some examples of swapping the signs. Mathematically, swapping the sign of the "i"s in a number is called "taking the complex conjugate", so Ed's explanation tells us that if we take the complex conjugate of the entirety of Maths, we'll get the same thing that we started with.
In Quantum Mechanics there are imaginary and complex numbers all over the place. Instead of describing things in 3D space with x, y and z being the units of length in each direction, we instead use what is called a Hilbert space, which allows us to use all manner of crazy things as our axes, and any number of them we want. In a complex Hilbert space, ie. a space where positions may include imaginary components, there is what's called a dual space, containing the complex conjugate of everything in the original space. Since taking the complex conjugate doesn't do anything as long as we do it consistently (ie. to everything) then any Hilbert space can be swapped with its dual and nothing about the Maths will change!
A closely related example is that when using Dirac's notation for Quantum Mechanics, we have a "bra" and a "ket" which together make a "braket". 'Bra A' looks like <A|, 'ket A' looks like |A> and a braket looks like <A|A>. The bras represent complex conjugates whilst the kets represent the original values, so <A| is the complex conjugate of |A>. Essentially bras and kets represent views into the Hilbert space and its dual: |A> is A as seen in the Hilbert space we're using, whilst <A| is A as seen in the dual space. Since we can swap the Hilbert space and dual space, we can use bras instead of kets and kets instead of bras and get the same answers to our calculations.
Another interesting use of complex conjugates is in the transactional interpretation of Quantum Mechanics. Quantum Mechanics involves lots of funky Maths, which works, but when people look for stories they can tell about what the Maths is doing (for example, if BBC's Horizon wants a voice-over to an irrelevant analogy) then there are several ways of explaining it. A nice idea is the transactional interpretation, where Schroedinger's equation (which describes how a quantum system changes over time) and its complex conjugate (which arises due to relativity) are both taken to be actual Physical laws. In other interpretations, the complex conjugate form is discarded as unphysical (like Ed tried to initially do with the red laser equation), leaving the Schroedinger equation to describe the movement of waves over time. This is a bit of a rubbish thing to do though, since we know that our imaginary units represent the same quantities, so we'd like a solution which doesn't involve throwing away whichever imaginary 'direction' is inconvenient. If we do keep the complex conjugate version then we get a second equation describing the movement of waves backwards in time, which is pretty peculiar but we're just upright apes so that's no reason to stop investigating.
The transactional interpretation of Quantum Mechanics shows that every event sends waves forwards and backwards in time, for example the emmission or absorbtion of radiation. However, we don't see these "waves from the future" since they stack up on top of each other and end up cancelling each other out. For example, an electron emits radiation and sends it forwards and backwards in time. Later on an electron absorbs this radiation and it too sends waves forwards and backwards in time. The forwards-in-time wave given out by the absorbtion exactly cancels with the forward-in-time wave given out by the emission, so at times after the absorbtion, the waves cancel to nothing. Likewise the backwards-in-time waves cancel for all times before the emmission, so there's nothing about an event which exists before it occurs (since the waves, when multiplied by their ocmplex conjugate, give probabilities. If the waves cancel to zero then the probability of anything to do with the wave existing at that point is zero). In the time between emmission and absorbtion, there is a wave travelling forwards in time and a wave travelling backwards in time, which turn out not to cancel, and we see one wave (the sum of the two) as we travel along in time. This is nice since we can swap the "i"s for "-i"s and get the same results, we'd just change the direction in time we're travelling in from "forwards" to "backwards", but like the +N and -N of Ed Daw's example, we've just made up those concepts as if they mean something. The reality is that there's no way of making such a distinction, so it becomes meaningless to try and find the values of "+N", "-N", "forwards" or "backwards". Just choose one and stick to it, like we normally choose "i" to be the positive root and "forward" to be the direction we perceive as our neurons interact thermodynamically.
Monday, 27 April 2009
Some Nice Things
I've not posted for a while, due to a mixture of an increasing workload, the ability to let off a constant barrage of my thoughts to Identi.ca rather than build them up into a blog post, and my constant disdain for Web-based apps.
So what do I want to blog about? Nothing particularly structured, just some stuff that I find interesting. Keep in mind though, that my definition of interesting includes the fact that 12cm optical discs have increased their storage capacity by 2 orders of magnitude in the 27 years from the CD to the BluRay, whilst in the same time frame the capacity of 3 1/2" hard drives has gone up 12 orders of magnitude. (I'm writing an essay on Optical Data Storage for a Physics module :) )
For those of you who may remember Deluxe Paint on AGA capable Amigas I can heartily recommend that you check out Grafx2, which seems to work on pretty much every OS and has recently been added to Debian, so you can install it by ticking "grafx2" in any package manager, it will be downloaded and installed along with everything it depends on :) Doesn't seem to do animation yet, as far as I can tell, which is a shame.
Also recently added to Debian is Closed World Model, cwm. This is pretty special, since it takes cutting edge computer knowledge representation as used by the Semantic Web, and makes it accessible via a tool similar to UNIX's (and of course GNU's) classic sed tool. For example, you can use a command like "cwm --rdf inputfile1.rdf inputfile2.rdf --n3 inputfile3.n --rdf --think --pipe > output.rdf" to take at all of the knowledge from the RDF files inputfile1.rdf, inputfile2.rdf and inputfile3.n (in RDF-XML and Notation3 formats), comparing the knowledge they contain, and dumping all of the new knowledge it can infer into the RDF-XML file output.rdf. For example, inputfile1.rdf could contain statements that Chris Warburton is a student, Chris Warburton has a website http://www.freewebs.com/chriswarbo and that Chris Warburton has a brother David Warburton. inputfile2.rdf could say that Brothers are related and that Brothers share a Mother. inputfile3.n could say that David Warburton has a blog at http://fun-chips.blogspot.com and David Warburton has a mother Cheryl Warburton. cwd would then combine these and the output file would contain deductions such as David Warburton is related to a student, http://www.freewebs.com/chriswarbo is run by a student and Chris Warburton has a mother Cheryl Warburton.
This is pretty cool, since it commoditises the previously tricky area of RDF access, allowing it to be scripted, for example in the backend of Web sites, in the same way that Imagemagick has done to images (eg. for thumbnailing).
Pretty cool. Anyway, it's getting late so I should get some sleep now.
I'm going to post some of my programming experiments soon, so look out for them :)
Friday, 5 September 2008
Physics + Programming = Pretty
Whilst looking for a better-than-mine Python implementation of attractive-and-repulsive-based-on-the-inverse-square-law particle simulation I came across this, which is basically a really simple model of gravity. You tell it how many balls you want it to start with, which are then placed at random points on the screen with zero momentum and a mass of 4. Then the simulation starts, running one time step of the simulation and redrawing the screen, then repeating this indefinitely. Particles which collide coalesce into a single particle with the combined mass and momentum of the original. This results in one of three things happening, either all of the masses coalesce into a big, stationary ball (since the net momentum is zero, due to the law of conservation of momentum), two or more masses form a somewhat stable orbit around each other, or one or masses hit the edge of the window during the simulation and 'reflect' (the vector of their velocity perpendicular to the edge is reversed) which breaks the physical simulation by violating conservation of momentum. After this third scenario all hell can break loose, usually resulting in everything coalescing into a huge ball, moving with momentum twice the magnitude of that which was flipped by hitting the wall, and opposite in direction.
Anyway, I looked through the short source file and had a bit of a play. Eventually I gave particles a colour which changes subtley every time they are drawn. I also disabled the old-frame-removing screen fill, allowing each frame of the animation to build upon the previous and create a trail. A little simple colour-cycle logic and I the following patterns appeared to my delight :D
HERE'S THE SOURCE (not properly licensed due to original author. Let's say you can treat is as Public Domain to save complications of licenses)
Anyway, I looked through the short source file and had a bit of a play. Eventually I gave particles a colour which changes subtley every time they are drawn. I also disabled the old-frame-removing screen fill, allowing each frame of the animation to build upon the previous and create a trail. A little simple colour-cycle logic and I the following patterns appeared to my delight :D
HERE'S THE SOURCE (not properly licensed due to original author. Let's say you can treat is as Public Domain to save complications of licenses)
Coming down to Earth with Physics
I read a blog post today where the writer imagined future computers being capable of unlimited calculations, storage, etc.
To quote the author: "Electricity and other force waves can be “on” or “off”, but they also have lots of other properties, many of which are sufficient to represent an infinity (or near-infinity). Frequency of any wave represents an infinity, for example–you can have a 1 Hz wave, a 1.1 Hz wave, a 1.15 Hz wave, a 1.151 Hz wave, etc.".
Disregarding the nonsense term "near-infinity", here an assumption has been made that waves have a continuous spectrum of frequencies, so that another decimal can always be added and allow ten times the number of frequencies to be used. Is this assumption valid? Physics says no. The frequency of a wave is equal to the energy of the wave divided by Planck's constant (f = E/h). Since Planck's constant is constant, for a wave to have a continuous spread of frequencies it must have a continuous spread of energies. Quantum mechanics shows us that energy occurs only in certain quantities ("quantity" making it "quantum"), for a very simple example see the quantum harmonic oscillator.
The author also states "the fact that waves take up essentially no space (only the medium that they vibrate takes up space)." To me this represents a complete misunderstanding of what a wave actually is. Wikipedia defines a wave as:
"A wave is a disturbance that propagates through space and time, usually with transference of energy. While a mechanical wave exists in a medium (which on deformation is capable of producing elastic restoring forces), waves of electromagnetic radiation (and probably gravitational radiation) can travel through vacuum, that is, without a medium. Waves travel and transfer energy from one point to another, often with little or no permanent displacement of the particles of the medium (that is, with little or no associated mass transport); instead there are oscillations around almost fixed locations."
Notice that two contradictions to the blog author appear here. Firstly the definition includes, straight away, the word space. Without space there are no waves. Secondly waves do not necessarily need a medium to exist in. A wave is not an entity of itself, it is an abstract concept which describes the oscillation of something.
To quote the author: "Electricity and other force waves can be “on” or “off”, but they also have lots of other properties, many of which are sufficient to represent an infinity (or near-infinity). Frequency of any wave represents an infinity, for example–you can have a 1 Hz wave, a 1.1 Hz wave, a 1.15 Hz wave, a 1.151 Hz wave, etc.".
Disregarding the nonsense term "near-infinity", here an assumption has been made that waves have a continuous spectrum of frequencies, so that another decimal can always be added and allow ten times the number of frequencies to be used. Is this assumption valid? Physics says no. The frequency of a wave is equal to the energy of the wave divided by Planck's constant (f = E/h). Since Planck's constant is constant, for a wave to have a continuous spread of frequencies it must have a continuous spread of energies. Quantum mechanics shows us that energy occurs only in certain quantities ("quantity" making it "quantum"), for a very simple example see the quantum harmonic oscillator.
The author also states "the fact that waves take up essentially no space (only the medium that they vibrate takes up space)." To me this represents a complete misunderstanding of what a wave actually is. Wikipedia defines a wave as:
"A wave is a disturbance that propagates through space and time, usually with transference of energy. While a mechanical wave exists in a medium (which on deformation is capable of producing elastic restoring forces), waves of electromagnetic radiation (and probably gravitational radiation) can travel through vacuum, that is, without a medium. Waves travel and transfer energy from one point to another, often with little or no permanent displacement of the particles of the medium (that is, with little or no associated mass transport); instead there are oscillations around almost fixed locations."
Notice that two contradictions to the blog author appear here. Firstly the definition includes, straight away, the word space. Without space there are no waves. Secondly waves do not necessarily need a medium to exist in. A wave is not an entity of itself, it is an abstract concept which describes the oscillation of something.
Add to this the fact that analogue systems (ie. continuous valued measurables) suffer from noise in a non-recoverable way (unlike digital systems), which makes your measuring device limited to its resolving power, which once again is limited thanks to the effect of apertures (the smaller the worse, by the way, making smaller spaces less distinguishable), and this whole concept, whilst initially sciencey-sounding, is unfortunately a no-starter.
Friday, 16 November 2007
Dir En Get Out Of My House
I went to see Dir Emo Grey yesterday. Wow. I wrote up a mini-report of the evening on the Sheffield RockSoc forum:
Well, that was damned awful Smile
After a Gestapo search for cameras and recording equipment, half a million statements about cameras not being allowed but NOT ONE request/form/statement/whatever about me giving consent and permission for their authorised photographers to film/photograph me, we got in and smiled at some of the sillier outfits. Then Raging Speedhorn came on and started shouting at me, which wasn't very nice (I couldn't tell what they were saying, but Emma and I agreed it was probably about rainbows, unicorns and kittens). They left and things got really disturbing.
Every time a stage hand came on to setup a microphone or something everyone started going conpletely insane. That kind of fanatacism is scary, and needs help. Anyway, Dir En Grey came on and I found it amusing how powerful the crowd's collective cheer was. They started playing some pretty below average sounding songs (well, they were below average after I blocked out the vocalist, who had also decided to shout at me. With him they were terrible). Disregarding the headbutting I got I thought it was pretty amusing (well, topless Japanese men shouting at high pitches whilst headbanging with tshirts over their heads generally are), and the vocalist guy's got a really hot body. Plus there was a guy with waist-length hair whirlwinding next to me which made a nice breeze. Then though, the vocalist got up on one of the stage gizmos and started slashing at his chest the stupid emo whore (amid my disgust I did manage to giggle when he couldn't even get it right). All of the bopping little girls were cheering him on, as if it's something cool, then all the lights went down and everyone went quiet since it was meant to be really deep and meaningful or something, so I shouted "EMO!" as loud as I could and went to get some water. I looked across after and saw the vocalist was spazzing out which made me laugh quite a bit (it reminded me of Elliot), then I left since I wasn't going to endorse that kind of obnoxious disregard for responsibility (I'd already lost Emma amid the crowd by that point, and there was no way to get back to the front after I'd got a drink).
I walked up the road and got complemented by some guy about my hair (he said his wife would love it and I should go on X Factor). He shook my hand after I told him I'd rather die than go on X Factor, then I went to the Devonshire Chippy and got a spring roll and chips (chips >= self harm) and waited outside Corp for Emma.
So yes, all in all I was pretty disgusted. I quite liked having a load of female bodies pressed against me (I couldn't bop along myself at the beginnning or else the girl in front of me would think I was trying to anally rape her), since it reminded me of Saturday nights, but I was outraged that some of them might give in to that twisted brainwashing (based on their reaction to the stage crew and the "you're not allowed cameras" people I would say they've already been warped quite a bit) and then get home and harm themselves (probably on a webcam or something too, which would make it worse. Then to rub salt in they'd be broadcasting it using that Microsoft MSN Hotmail Live Windows Messenger Vista thingy). It reminded me of a public execution, but where people were going "Wow, that guy is so cool". Trying to pass that stunt off as art made me die a little inside, and made the bits left alive get angry.
My thoughts on Dir En Grey? Well, if you know someone who doesn't like themselves and you really don't like them either and think that the world would be a better place if they stopped whining on and on about the emotional crap that they think they're going through but actually have no idea about and just shot themselves already then I think it would be a good recommendation to get them to see. If, however, you know someone like that who you DO like, or at least don't dislike enough to wish them dead, then in your shoes I would do everything in my power to stop them getting drawn further and further in and down that ridiculously merciless spiral, part of which is wanting to listen to people screaming then idolising them when they go "You think I'm cool now? Wait until you see this!" *miss attempt to cut onesself* *miss again* *miss again* *actually manage it* *put tshirt on head and spasm out in the manner of an epileptic fit*. If you don't know anyone like that but want to, then pop along and maybe get yourself some underage emo pussy (get a friend to tell them they're fat or something, then they'll assume 1) it's true and 2) that it's a bad thing and then they'll turn on their emo powers, at which point you can step in to offer an understanding shoulder to cry on, then you're in (maybe I should stop going off on disturbing tangents?)). If you don't fit into any of those catagories then I suggest you go to the Devonshire Chippy and the nice guy in there will sell you some chips and spring rolls (and Chicken and Mushroom pies, depending on what you fancy) then impress you with his chip fork flourishes, then amuse you by picking your change up off the floor after failing his money flourish, plus he'll give you water if your friend is feinting outside, unlike the bastards at the wannabe-trendy place next door.
The best thing about tonight? I didn't pay, and thus was not condoning such a blatant display of consumerist culture's ugly reality.
Feel free to reply, but I don't come in here often since forums are just bastardised versions of mailing lists which have no place inside a web browser.
So yes. I really would urge you not to endorse them. Apathy can die in a bin as far as I'm concerned.
I handed in my Physics work today which was nice.
I've also been spicing up my laptop with funky 3D effects. I'm trying out the Avant Window Navigator, which is a big fat rip off of Mac OSX's dock. HOWEVER, it does reduce desktop redundancy which is nice. It doesn't seem to have a very useful system tray, which means I would lose a bit of functionality if I used it exclusively, and also whenever I drag a desktop launcher onto AWN it never seems to stay in place.
The reduction in redundancy is seriously VERY nice. Blingy too (I have the "squishy" effect on, which is the same as the KDE launcher effect next to my mouse pointer :P )
I am using Emerald with Compiz, since emulating Metacity makes me feel dirty. I also have Xwinwrap displaying the glslideshow screensaver for my desktop (although that occasionally quits :( I'll have to look through the options, or if the worst comes to the worst run it in a perpetual for loop). Quite impressive I must say. Plus it is still rather subtle (well, compared to the Airplane effect in Compiz that is :P )
Now I want them to fix the window-flashes-up-momentarily bug that has appeared for some of the effects (which means I can't use Burn on my drop down menus at the moment)
In slightly more productive computer news I'm trying to create an extensible physics simulator for use (amongst other things) on the XO laptop. I'm currently getting help from the developers to get an emulated system up and running (I tried the standard build image but it keeps resetting X at login when I run it in QEMU, KVM doesn't even get very far into the boot process and VirtualBox ONLY supports VMWare-style hard drive thingies, rather than allowing raw images to be used). I'll see if eToys works for me now (it didn't used to) and play around. If it looks good enough to build on then I'll do that, if not then I'll write a new one in Python.
Anyway, that's all for now. I'll be booking rooms tomorrow for a Free Software Society installfest. Should be good hopefully :)
Subscribe to:
Posts (Atom)
