Saturday, 22 January 2011
Enigma Number 1628
The question is this: raising a number to the power of itself is like 5 to the power of 5, or 5**5 in Python; a 'reverse' number is a number with its digits backwards, so 45 is the reverse of 54; a number that ends with another means that the least significant digits of the former are the same as all of the digits of the latter in the same order. Given this, what is the 2 digit number x such that x raised to the power of x ends with x, the reverse of x raised to the reverse of x ends with the reverse of x, the reverse of x raised to the power of x ends with the reverse of x and the digits in x aren't the same?
Translating this into Python is quite simple. We start with all of the possible answers, ie. the numbers 00-99, which we get via range(100). Next we can split them into a pair of the "tens and units" as they used to say in primary school. We do this with [(a/10,a%10) for a in range(100)]. Next we can put these back into a list of numbers by undoing the separation of the digits, like this [x*10+y for x,y in [(a/10,a%10) for a in range(100)]]. Next we want to put our filters on this. Namely, the 2 digits x and y cannot be equal, so x!=y; the number raised to itself, (x*10+y)**(x*10+y), must ends with itself, ie. ((x*10+y)**(x*10+y))%100==x*10+y; the same must be true for the reverse, where we just swap x and y; and the reverse to the power of the number, (y*10+x)**(x*10+y), must end in the reverse, y*10+x, so ((y*10+x)**(x*10+y))%100==y*10+x. Putting it all together we get a list of answers:
[x*10+y for x,y in [(a/10,a%10) for a in range(100)] if x!=y and ((x*10+y)**(x*10+y))%100==(x*10+y) and ((y*10+x)**(y*10+x))%100==(y*10+x) and ((y*10+x)**(x*10+y))%100==(y*10+x)]
Easy :)
PS: The answers are 16, 61 and 57
The question is this: raising a number to the power of itself is like 5 to the power of 5, or 5**5 in Python; a 'reverse' number is a number with its digits backwards, so 45 is the reverse of 54; a number that ends with another means that the least significant digits of the former are the same as all of the digits of the latter in the same order. Given this, what is the 2 digit number x such that x raised to the power of x ends with x, the reverse of x raised to the reverse of x ends with the reverse of x, the reverse of x raised to the power of x ends with the reverse of x and the digits in x aren't the same?
Translating this into Python is quite simple. We start with all of the possible answers, ie. the numbers 00-99, which we get via range(100). Next we can split them into a pair of the "tens and units" as they used to say in primary school. We do this with [(a/10,a%10) for a in range(100)]. Next we can put these back into a list of numbers by undoing the separation of the digits, like this [x*10+y for x,y in [(a/10,a%10) for a in range(100)]]. Next we want to put our filters on this. Namely, the 2 digits x and y cannot be equal, so x!=y; the number raised to itself, (x*10+y)**(x*10+y), must ends with itself, ie. ((x*10+y)**(x*10+y))%100==x*10+y; the same must be true for the reverse, where we just swap x and y; and the reverse to the power of the number, (y*10+x)**(x*10+y), must end in the reverse, y*10+x, so ((y*10+x)**(x*10+y))%100==y*10+x. Putting it all together we get a list of answers:
[x*10+y for x,y in [(a/10,a%10) for a in range(100)] if x!=y and ((x*10+y)**(x*10+y))%100==(x*10+y) and ((y*10+x)**(y*10+x))%100==(y*10+x) and ((y*10+x)**(x*10+y))%100==(y*10+x)]
Easy :)
PS: The answers are 16, 61 and 57
Thursday, 9 December 2010
Blog Dump 5: Some Statistics
#!/usr/bin/env python
import random
def flip():
"""Simulate a coin flip."""
if random.randint(0,1): # Choose this statement or the next with equal chance
return "Heads" # Give a "Heads"
else:
return "Tails" # Give a "Tails"
def lottery():
"""Run a St Petersburg Lottery, flipping a coin until it's tails. Each time it's heads
our pot is doubled and added to the running total."""
winnings = 1 # Start with 1 pound
pot = 1 # The pot starts at 1 pound
while flip() == "Heads": # Loop until we get a Tails
pot = pot * 2 # Double the pot
winnings = winnings + pot # Add it to our winnings
return winnings # When we've finished looping, return the result
def play(rounds):
"""Run the lottery 'rounds' times in a row."""
cost_per_game = 2 # Deduct this from the wealth for each round
wealth = 1 # Start with 1 pound
print "Rounds, Wealth" # Column headings for our spreadsheet
print "0,1" # Print the first results
for x in range(rounds): # Loop through each round
wealth = wealth - cost_per_game + lottery() # Deduct the cost and add the winnings to our wealth
print str(x+1)+', '+str(wealth) # Print the round number and our current wealth
The scenario is that we start with £1 and pay a fixed sum (here £2) to play a lottery, in which a coin if tossed. If it's tails then we take the

I've also made some simulations of the Monty Hall problem, random walks (intersecting and non-intersecting) and a few other statistical phenomena. I might post them if I get time. They can be the source of pretty patterns :)
#!/usr/bin/env python
import random
def flip():
"""Simulate a coin flip."""
if random.randint(0,1): # Choose this statement or the next with equal chance
return "Heads" # Give a "Heads"
else:
return "Tails" # Give a "Tails"
def lottery():
"""Run a St Petersburg Lottery, flipping a coin until it's tails. Each time it's heads
our pot is doubled and added to the running total."""
winnings = 1 # Start with 1 pound
pot = 1 # The pot starts at 1 pound
while flip() == "Heads": # Loop until we get a Tails
pot = pot * 2 # Double the pot
winnings = winnings + pot # Add it to our winnings
return winnings # When we've finished looping, return the result
def play(rounds):
"""Run the lottery 'rounds' times in a row."""
cost_per_game = 2 # Deduct this from the wealth for each round
wealth = 1 # Start with 1 pound
print "Rounds, Wealth" # Column headings for our spreadsheet
print "0,1" # Print the first results
for x in range(rounds): # Loop through each round
wealth = wealth - cost_per_game + lottery() # Deduct the cost and add the winnings to our wealth
print str(x+1)+', '+str(wealth) # Print the round number and our current wealth
The scenario is that we start with £1 and pay a fixed sum (here £2) to play a lottery, in which a coin if tossed. If it's tails then we take the

I've also made some simulations of the Monty Hall problem, random walks (intersecting and non-intersecting) and a few other statistical phenomena. I might post them if I get time. They can be the source of pretty patterns :)
Friday, 26 March 2010
Divergence and reduction with complex numbers
If you don't know what an imaginary number or a complex number is then don't worry. That link provides quite a nice intro, and I'll give my own here:
An "imaginary" number is a number which doesn't fit anywhere on the number line. No matter how closely you zoom in, or how far along you go, you'll never find it. That's why they're called "imaginary", even though it is an unfortunate name as the other blog points out. Before you dismiss imaginary numbers as useless, let's consider another set of numbers which is made up and doesn't exist in the real world: negative numbers.
Negative numbers cannot exist like the natural (positive) numbers do. You cannot have -5 apples. Nevertheless, negative numbers are useful for made up mathematical worlds, like banking for example, which can have a definite impact on the real, physical world. Negative numbers also arise in situations involving symmetry, relative values and arbitraryness. Let's take a realistic example: if we think of positions, there is no set of coordinate axes in the physical world, and the whole Universe is symmetric spatially, so we can just make up the numbers we use to be anything we find convenient. Let's say we've got a chocolate bar:
 We'd like to be able to refer to each section of chocolate in a unique way, so we can say that the bottom left section is at position (0,0), and define our unit of length to be one chocolate section. Thus we can say "The sections at (0,2) and (0,3) have been bitten". Now let's say that Dr Ed Daw has had a busy day and didn't have chance to grab some food. He's so hungry that he doesn't have enough energy to move more than one unit of distance to get the food he needs, but he spies our chocolate bar. Can Dr Daw get the food he needs?:
We'd like to be able to refer to each section of chocolate in a unique way, so we can say that the bottom left section is at position (0,0), and define our unit of length to be one chocolate section. Thus we can say "The sections at (0,2) and (0,3) have been bitten". Now let's say that Dr Ed Daw has had a busy day and didn't have chance to grab some food. He's so hungry that he doesn't have enough energy to move more than one unit of distance to get the food he needs, but he spies our chocolate bar. Can Dr Daw get the food he needs?: To find the distance between the doctor and the chocolate we need to know the doctor's position. We can't use a positive number to define the position, since even though there are an infinite number of them, they get less and less accurate the further we look. Instead we have to use a negative number, allowing us to say that Dr Ed Daw is at position (0, -1). We know there is chocolate at (0,0), so to get from his position to the food only takes one unit of distance, since (0,-1)+(0,1)=(0,0). The only reason we had to use a negative number here is because of the way we defined our mathematical model of the situation. There's no such thing as "negative position", but when we used the doctor's negative position to find the distance he has to move, which is a physical quantity, the negative numbers disappeared and we got a meaningful, and correct, answer.
To find the distance between the doctor and the chocolate we need to know the doctor's position. We can't use a positive number to define the position, since even though there are an infinite number of them, they get less and less accurate the further we look. Instead we have to use a negative number, allowing us to say that Dr Ed Daw is at position (0, -1). We know there is chocolate at (0,0), so to get from his position to the food only takes one unit of distance, since (0,-1)+(0,1)=(0,0). The only reason we had to use a negative number here is because of the way we defined our mathematical model of the situation. There's no such thing as "negative position", but when we used the doctor's negative position to find the distance he has to move, which is a physical quantity, the negative numbers disappeared and we got a meaningful, and correct, answer.So let's move on to imaginary numbers: Close to the surface of the Earth, gravity is pretty constant, with a value of 9.81 metres per second per second. This means that vertical speed (metres per second, miles per hour, etc.) will go down by 9.81 metres per second (if it's pointing up), or up by 9.81 metres per second (if it's pointing down) every second. Speed describes how your position changes in time (eg. how many metres you move in a second), so the position of something flying through the air will change by the speed which itself will change due to gravity, so the position will curve. The shapes made by these curves are called parabolas and behave like the quantity -Ax^2 + Bx + C, where x is your horizontal position (or you could use time here instead) and A, B and C are numbers specific to what you're looking at. We get a minus sign for the x^2 because gravity points down and we define up to be positive. If we want to know at what position or time a ballistic (falling) object will reach a certain height, what we're really asking is at what position or time does Ax^2 + Bx + C equal the height we're interested in. We can do this with an example: Dr Daw has finished his chocolate and is trying to show off some lasers to his younger, more tanned brother. They each attach a laser to their head, Ed takes the red one and his brother De takes the green one. The lasers need to be kept cool, so they go to the Sheffield Ski Village. While they watch the skiers go past, De asks his brother "When do the skiers get higher than the lasers attached to our heads?". How can Ed work this out, given that the skiers motion can be described by -x^2 + 0x + 5, that De's green laser is a height of 4 and that Ed's red laser is at a height of 6?
 Ed knows that he can take the skiers's motion and, using the apex of the jump as position 0, work our at which positions they get above the lasers by saying -x^2 + 5 = 4 when they get above De's laser and -x^2 + 5 = 6 when they cross his laser. Working out the first gives the valid positions, x, as:
Ed knows that he can take the skiers's motion and, using the apex of the jump as position 0, work our at which positions they get above the lasers by saying -x^2 + 5 = 4 when they get above De's laser and -x^2 + 5 = 6 when they cross his laser. Working out the first gives the valid positions, x, as:-x^2 + 5 = 4
-x^2 = 4 - 5
-x^2 = -1
x^2 = 1
x = +1 or -1
He tells his brother that the skiers will cross the green laser at positions -1 and +1, since they satisfy the equation of motion. He then tries to work out when they cross the red laser:
-x^2 + 5 = 6
-x^2 = 6 - 5
-x^2 = 1
x^2 = -1
Then Ed gets stuck, since there's no positive or negative number he can think of which would fit as x here. Thus he declares to De "There are no solutions, so the skiers never get above my laser.". De is not satisfied with this. He says "That's cheating. I want you to finish working it out.". Ed knows how stubborn his brother is, since he carried on wearing fake tan even after going on "Snog, Marry, Avoid" the previous year, so he invents a number to satisft this equation:
"The skiers cross my laser whenever they get to a position which I will call N. They will also cross the laser if they get to a position -N. Thus, +N and -N are the solutions to this equation."
De is still not satisfied, so he asks his brother what N is. The doctor then explains imaginary numbers to the younger man:
"N is a quantity that is not a positive number, or a negative number, however it is a very useful quantity, since it lets us solve the equation for my laser. You can't find it no matter how closely you look between the numbers, or how far along you go. This means that its value is orthogonal to the real numbers, since the two are independent, in the same way that you can't change an x coordinate by moving in the y direction. In fact, we could draw a diagram using the real numbers as an x axis and these imaginary ones as the y axis."
"I'm confused." said De, "Will you please draw me such a diagram?"
"I can't be arsed," Ed replied, "so here's one I found on Wikipedia."
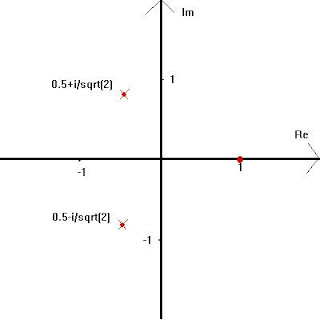 Using this diagram, Ed could explain to his brother how a Real number (Re) sits on the horizontal line, how an Imaginary number (Im) sits on the vertical line, and how the quadrants are filled with numbers that have an imaginary part and a real part, and are called Complex numbers. De seemed to understand, but had some questions:
Using this diagram, Ed could explain to his brother how a Real number (Re) sits on the horizontal line, how an Imaginary number (Im) sits on the vertical line, and how the quadrants are filled with numbers that have an imaginary part and a real part, and are called Complex numbers. De seemed to understand, but had some questions:"OK, I'll accept what you just said, but then where does our quantity N fit in this diagram? Also, there are some undefined variables; what is the value of the "i" that's written on the diagram?"
"The "i" represents the Imaginary unit." Ed explained, "It's equivalent to the number 1 for natural numbers, and -1 for negative numbers. Every Imaginary number is made out of some quantity of i."
"So what is the value of i?"
"The imaginary unit is defined by the equation i^2 = -1. No more, no less."
"But that's the equation for the skiers crossing your laser! That means that N = i and the skiers will cross if they ever get to a position i, which they can never do because imaginary space is orthogonal to physical space, so no force can ever push them off the Real lines for x, y and z."
"Well done" said an impressed Ed "but you're forgetting how to do square roots! There are always two square roots of a number, just like we had +N and -N. That means that i^2 = -1 and (-i)^2 = -1. So tell me, does N = i or does N = -i?"
De thought about this for a minute before declaring "There's no way of telling! If N = i then N^2 = -1 since i^2 = -1, but also (-N)^2 = -1 since the minus signs cancel so -N = i. But also, (-i)^2 = -1 so N = -i and, because the minus signs cancel, i^2 = -1, so N = i. So N = +i or -i and -N = +i or -i, they're equal!"
"Don't be too hasty to call them equal!" cautioned Ed "If N = -N then i = -i and I could do the following:
i = -i This is what you are claiming
i + i = -i + i We can add i to each side to preserve the equality
2i = 0 Adding i to i gives 2i, whilst adding i to -i gives zero
i = 0 We can divide both sides by 2 and preserve the equality
i*i = 0*i We can multiply each side by i and preserve the equality
i*i = 0*0 We showed that i=0 so use that on the right hand side
i*i = 0 We know 0*0=0
-1 = 0 From the definition of i, i*i = -1
We have reached an absurdity! The only conclusion is that i cannot be equal to -i, and thus N cannot be equal to -N."
"So which way around are they?" implored De.
"It's unknowable." replied Ed, "You can use either i = N or i = -N and you'll get the same results. Swapping every i for a -i in any Maths will change nothing, as long as you're consistent in which value (i or -i) you take to be positive. By convention we say that i is positive, and that -i is negative, but that's just a sentence in this silly human language of ours. It has no mathematical meaning, since they are both the imaginary unit, whilst also being distinct and not equal."
"Fascinating!" exclaimed De, "Can you give me some examples of swapping i and -i?"
"No." said Ed stubbornly, "We've taken this example far too off course, so we'll leave Chris to explain that. Now let's take these lasers back to the Hicks before Professor Fox realises we've taken them!"
Q.E.D.
So, why is having two imaginary roots cool? Well, just as in the case of negative numbers, where the physical quantities like length always end up positive despite our use of negative numbers in our made up mathematical models, similarly every physical quantity calculated using imaginary numbers turns out to be real, and furthermore it turns out the same no matter whether you use i as your basic unit of imaginaryness or -i. They both represent the same unknowable pair of imaginary quantities that Ed called +N and -N, and since we can never know the "N"s we may as well use the "i"s, and just treat them as algebraic names (like we would "x" or "p" or any other variable name), and always keep in mind that the equation i^2 = -1 is simultaneous to everything we do.
So on to some examples of swapping the signs. Mathematically, swapping the sign of the "i"s in a number is called "taking the complex conjugate", so Ed's explanation tells us that if we take the complex conjugate of the entirety of Maths, we'll get the same thing that we started with.
In Quantum Mechanics there are imaginary and complex numbers all over the place. Instead of describing things in 3D space with x, y and z being the units of length in each direction, we instead use what is called a Hilbert space, which allows us to use all manner of crazy things as our axes, and any number of them we want. In a complex Hilbert space, ie. a space where positions may include imaginary components, there is what's called a dual space, containing the complex conjugate of everything in the original space. Since taking the complex conjugate doesn't do anything as long as we do it consistently (ie. to everything) then any Hilbert space can be swapped with its dual and nothing about the Maths will change!
A closely related example is that when using Dirac's notation for Quantum Mechanics, we have a "bra" and a "ket" which together make a "braket". 'Bra A' looks like <A|, 'ket A' looks like |A> and a braket looks like <A|A>. The bras represent complex conjugates whilst the kets represent the original values, so <A| is the complex conjugate of |A>. Essentially bras and kets represent views into the Hilbert space and its dual: |A> is A as seen in the Hilbert space we're using, whilst <A| is A as seen in the dual space. Since we can swap the Hilbert space and dual space, we can use bras instead of kets and kets instead of bras and get the same answers to our calculations.
Another interesting use of complex conjugates is in the transactional interpretation of Quantum Mechanics. Quantum Mechanics involves lots of funky Maths, which works, but when people look for stories they can tell about what the Maths is doing (for example, if BBC's Horizon wants a voice-over to an irrelevant analogy) then there are several ways of explaining it. A nice idea is the transactional interpretation, where Schroedinger's equation (which describes how a quantum system changes over time) and its complex conjugate (which arises due to relativity) are both taken to be actual Physical laws. In other interpretations, the complex conjugate form is discarded as unphysical (like Ed tried to initially do with the red laser equation), leaving the Schroedinger equation to describe the movement of waves over time. This is a bit of a rubbish thing to do though, since we know that our imaginary units represent the same quantities, so we'd like a solution which doesn't involve throwing away whichever imaginary 'direction' is inconvenient. If we do keep the complex conjugate version then we get a second equation describing the movement of waves backwards in time, which is pretty peculiar but we're just upright apes so that's no reason to stop investigating.
The transactional interpretation of Quantum Mechanics shows that every event sends waves forwards and backwards in time, for example the emmission or absorbtion of radiation. However, we don't see these "waves from the future" since they stack up on top of each other and end up cancelling each other out. For example, an electron emits radiation and sends it forwards and backwards in time. Later on an electron absorbs this radiation and it too sends waves forwards and backwards in time. The forwards-in-time wave given out by the absorbtion exactly cancels with the forward-in-time wave given out by the emission, so at times after the absorbtion, the waves cancel to nothing. Likewise the backwards-in-time waves cancel for all times before the emmission, so there's nothing about an event which exists before it occurs (since the waves, when multiplied by their ocmplex conjugate, give probabilities. If the waves cancel to zero then the probability of anything to do with the wave existing at that point is zero). In the time between emmission and absorbtion, there is a wave travelling forwards in time and a wave travelling backwards in time, which turn out not to cancel, and we see one wave (the sum of the two) as we travel along in time. This is nice since we can swap the "i"s for "-i"s and get the same results, we'd just change the direction in time we're travelling in from "forwards" to "backwards", but like the +N and -N of Ed Daw's example, we've just made up those concepts as if they mean something. The reality is that there's no way of making such a distinction, so it becomes meaningless to try and find the values of "+N", "-N", "forwards" or "backwards". Just choose one and stick to it, like we normally choose "i" to be the positive root and "forward" to be the direction we perceive as our neurons interact thermodynamically.
If you don't know what an imaginary number or a complex number is then don't worry. That link provides quite a nice intro, and I'll give my own here:
An "imaginary" number is a number which doesn't fit anywhere on the number line. No matter how closely you zoom in, or how far along you go, you'll never find it. That's why they're called "imaginary", even though it is an unfortunate name as the other blog points out. Before you dismiss imaginary numbers as useless, let's consider another set of numbers which is made up and doesn't exist in the real world: negative numbers.
Negative numbers cannot exist like the natural (positive) numbers do. You cannot have -5 apples. Nevertheless, negative numbers are useful for made up mathematical worlds, like banking for example, which can have a definite impact on the real, physical world. Negative numbers also arise in situations involving symmetry, relative values and arbitraryness. Let's take a realistic example: if we think of positions, there is no set of coordinate axes in the physical world, and the whole Universe is symmetric spatially, so we can just make up the numbers we use to be anything we find convenient. Let's say we've got a chocolate bar:
 We'd like to be able to refer to each section of chocolate in a unique way, so we can say that the bottom left section is at position (0,0), and define our unit of length to be one chocolate section. Thus we can say "The sections at (0,2) and (0,3) have been bitten". Now let's say that Dr Ed Daw has had a busy day and didn't have chance to grab some food. He's so hungry that he doesn't have enough energy to move more than one unit of distance to get the food he needs, but he spies our chocolate bar. Can Dr Daw get the food he needs?:
We'd like to be able to refer to each section of chocolate in a unique way, so we can say that the bottom left section is at position (0,0), and define our unit of length to be one chocolate section. Thus we can say "The sections at (0,2) and (0,3) have been bitten". Now let's say that Dr Ed Daw has had a busy day and didn't have chance to grab some food. He's so hungry that he doesn't have enough energy to move more than one unit of distance to get the food he needs, but he spies our chocolate bar. Can Dr Daw get the food he needs?: To find the distance between the doctor and the chocolate we need to know the doctor's position. We can't use a positive number to define the position, since even though there are an infinite number of them, they get less and less accurate the further we look. Instead we have to use a negative number, allowing us to say that Dr Ed Daw is at position (0, -1). We know there is chocolate at (0,0), so to get from his position to the food only takes one unit of distance, since (0,-1)+(0,1)=(0,0). The only reason we had to use a negative number here is because of the way we defined our mathematical model of the situation. There's no such thing as "negative position", but when we used the doctor's negative position to find the distance he has to move, which is a physical quantity, the negative numbers disappeared and we got a meaningful, and correct, answer.
To find the distance between the doctor and the chocolate we need to know the doctor's position. We can't use a positive number to define the position, since even though there are an infinite number of them, they get less and less accurate the further we look. Instead we have to use a negative number, allowing us to say that Dr Ed Daw is at position (0, -1). We know there is chocolate at (0,0), so to get from his position to the food only takes one unit of distance, since (0,-1)+(0,1)=(0,0). The only reason we had to use a negative number here is because of the way we defined our mathematical model of the situation. There's no such thing as "negative position", but when we used the doctor's negative position to find the distance he has to move, which is a physical quantity, the negative numbers disappeared and we got a meaningful, and correct, answer.So let's move on to imaginary numbers: Close to the surface of the Earth, gravity is pretty constant, with a value of 9.81 metres per second per second. This means that vertical speed (metres per second, miles per hour, etc.) will go down by 9.81 metres per second (if it's pointing up), or up by 9.81 metres per second (if it's pointing down) every second. Speed describes how your position changes in time (eg. how many metres you move in a second), so the position of something flying through the air will change by the speed which itself will change due to gravity, so the position will curve. The shapes made by these curves are called parabolas and behave like the quantity -Ax^2 + Bx + C, where x is your horizontal position (or you could use time here instead) and A, B and C are numbers specific to what you're looking at. We get a minus sign for the x^2 because gravity points down and we define up to be positive. If we want to know at what position or time a ballistic (falling) object will reach a certain height, what we're really asking is at what position or time does Ax^2 + Bx + C equal the height we're interested in. We can do this with an example: Dr Daw has finished his chocolate and is trying to show off some lasers to his younger, more tanned brother. They each attach a laser to their head, Ed takes the red one and his brother De takes the green one. The lasers need to be kept cool, so they go to the Sheffield Ski Village. While they watch the skiers go past, De asks his brother "When do the skiers get higher than the lasers attached to our heads?". How can Ed work this out, given that the skiers motion can be described by -x^2 + 0x + 5, that De's green laser is a height of 4 and that Ed's red laser is at a height of 6?
 Ed knows that he can take the skiers's motion and, using the apex of the jump as position 0, work our at which positions they get above the lasers by saying -x^2 + 5 = 4 when they get above De's laser and -x^2 + 5 = 6 when they cross his laser. Working out the first gives the valid positions, x, as:
Ed knows that he can take the skiers's motion and, using the apex of the jump as position 0, work our at which positions they get above the lasers by saying -x^2 + 5 = 4 when they get above De's laser and -x^2 + 5 = 6 when they cross his laser. Working out the first gives the valid positions, x, as:-x^2 + 5 = 4
-x^2 = 4 - 5
-x^2 = -1
x^2 = 1
x = +1 or -1
He tells his brother that the skiers will cross the green laser at positions -1 and +1, since they satisfy the equation of motion. He then tries to work out when they cross the red laser:
-x^2 + 5 = 6
-x^2 = 6 - 5
-x^2 = 1
x^2 = -1
Then Ed gets stuck, since there's no positive or negative number he can think of which would fit as x here. Thus he declares to De "There are no solutions, so the skiers never get above my laser.". De is not satisfied with this. He says "That's cheating. I want you to finish working it out.". Ed knows how stubborn his brother is, since he carried on wearing fake tan even after going on "Snog, Marry, Avoid" the previous year, so he invents a number to satisft this equation:
"The skiers cross my laser whenever they get to a position which I will call N. They will also cross the laser if they get to a position -N. Thus, +N and -N are the solutions to this equation."
De is still not satisfied, so he asks his brother what N is. The doctor then explains imaginary numbers to the younger man:
"N is a quantity that is not a positive number, or a negative number, however it is a very useful quantity, since it lets us solve the equation for my laser. You can't find it no matter how closely you look between the numbers, or how far along you go. This means that its value is orthogonal to the real numbers, since the two are independent, in the same way that you can't change an x coordinate by moving in the y direction. In fact, we could draw a diagram using the real numbers as an x axis and these imaginary ones as the y axis."
"I'm confused." said De, "Will you please draw me such a diagram?"
"I can't be arsed," Ed replied, "so here's one I found on Wikipedia."
 Using this diagram, Ed could explain to his brother how a Real number (Re) sits on the horizontal line, how an Imaginary number (Im) sits on the vertical line, and how the quadrants are filled with numbers that have an imaginary part and a real part, and are called Complex numbers. De seemed to understand, but had some questions:
Using this diagram, Ed could explain to his brother how a Real number (Re) sits on the horizontal line, how an Imaginary number (Im) sits on the vertical line, and how the quadrants are filled with numbers that have an imaginary part and a real part, and are called Complex numbers. De seemed to understand, but had some questions:"OK, I'll accept what you just said, but then where does our quantity N fit in this diagram? Also, there are some undefined variables; what is the value of the "i" that's written on the diagram?"
"The "i" represents the Imaginary unit." Ed explained, "It's equivalent to the number 1 for natural numbers, and -1 for negative numbers. Every Imaginary number is made out of some quantity of i."
"So what is the value of i?"
"The imaginary unit is defined by the equation i^2 = -1. No more, no less."
"But that's the equation for the skiers crossing your laser! That means that N = i and the skiers will cross if they ever get to a position i, which they can never do because imaginary space is orthogonal to physical space, so no force can ever push them off the Real lines for x, y and z."
"Well done" said an impressed Ed "but you're forgetting how to do square roots! There are always two square roots of a number, just like we had +N and -N. That means that i^2 = -1 and (-i)^2 = -1. So tell me, does N = i or does N = -i?"
De thought about this for a minute before declaring "There's no way of telling! If N = i then N^2 = -1 since i^2 = -1, but also (-N)^2 = -1 since the minus signs cancel so -N = i. But also, (-i)^2 = -1 so N = -i and, because the minus signs cancel, i^2 = -1, so N = i. So N = +i or -i and -N = +i or -i, they're equal!"
"Don't be too hasty to call them equal!" cautioned Ed "If N = -N then i = -i and I could do the following:
i = -i This is what you are claiming
i + i = -i + i We can add i to each side to preserve the equality
2i = 0 Adding i to i gives 2i, whilst adding i to -i gives zero
i = 0 We can divide both sides by 2 and preserve the equality
i*i = 0*i We can multiply each side by i and preserve the equality
i*i = 0*0 We showed that i=0 so use that on the right hand side
i*i = 0 We know 0*0=0
-1 = 0 From the definition of i, i*i = -1
We have reached an absurdity! The only conclusion is that i cannot be equal to -i, and thus N cannot be equal to -N."
"So which way around are they?" implored De.
"It's unknowable." replied Ed, "You can use either i = N or i = -N and you'll get the same results. Swapping every i for a -i in any Maths will change nothing, as long as you're consistent in which value (i or -i) you take to be positive. By convention we say that i is positive, and that -i is negative, but that's just a sentence in this silly human language of ours. It has no mathematical meaning, since they are both the imaginary unit, whilst also being distinct and not equal."
"Fascinating!" exclaimed De, "Can you give me some examples of swapping i and -i?"
"No." said Ed stubbornly, "We've taken this example far too off course, so we'll leave Chris to explain that. Now let's take these lasers back to the Hicks before Professor Fox realises we've taken them!"
Q.E.D.
So, why is having two imaginary roots cool? Well, just as in the case of negative numbers, where the physical quantities like length always end up positive despite our use of negative numbers in our made up mathematical models, similarly every physical quantity calculated using imaginary numbers turns out to be real, and furthermore it turns out the same no matter whether you use i as your basic unit of imaginaryness or -i. They both represent the same unknowable pair of imaginary quantities that Ed called +N and -N, and since we can never know the "N"s we may as well use the "i"s, and just treat them as algebraic names (like we would "x" or "p" or any other variable name), and always keep in mind that the equation i^2 = -1 is simultaneous to everything we do.
So on to some examples of swapping the signs. Mathematically, swapping the sign of the "i"s in a number is called "taking the complex conjugate", so Ed's explanation tells us that if we take the complex conjugate of the entirety of Maths, we'll get the same thing that we started with.
In Quantum Mechanics there are imaginary and complex numbers all over the place. Instead of describing things in 3D space with x, y and z being the units of length in each direction, we instead use what is called a Hilbert space, which allows us to use all manner of crazy things as our axes, and any number of them we want. In a complex Hilbert space, ie. a space where positions may include imaginary components, there is what's called a dual space, containing the complex conjugate of everything in the original space. Since taking the complex conjugate doesn't do anything as long as we do it consistently (ie. to everything) then any Hilbert space can be swapped with its dual and nothing about the Maths will change!
A closely related example is that when using Dirac's notation for Quantum Mechanics, we have a "bra" and a "ket" which together make a "braket". 'Bra A' looks like <A|, 'ket A' looks like |A> and a braket looks like <A|A>. The bras represent complex conjugates whilst the kets represent the original values, so <A| is the complex conjugate of |A>. Essentially bras and kets represent views into the Hilbert space and its dual: |A> is A as seen in the Hilbert space we're using, whilst <A| is A as seen in the dual space. Since we can swap the Hilbert space and dual space, we can use bras instead of kets and kets instead of bras and get the same answers to our calculations.
Another interesting use of complex conjugates is in the transactional interpretation of Quantum Mechanics. Quantum Mechanics involves lots of funky Maths, which works, but when people look for stories they can tell about what the Maths is doing (for example, if BBC's Horizon wants a voice-over to an irrelevant analogy) then there are several ways of explaining it. A nice idea is the transactional interpretation, where Schroedinger's equation (which describes how a quantum system changes over time) and its complex conjugate (which arises due to relativity) are both taken to be actual Physical laws. In other interpretations, the complex conjugate form is discarded as unphysical (like Ed tried to initially do with the red laser equation), leaving the Schroedinger equation to describe the movement of waves over time. This is a bit of a rubbish thing to do though, since we know that our imaginary units represent the same quantities, so we'd like a solution which doesn't involve throwing away whichever imaginary 'direction' is inconvenient. If we do keep the complex conjugate version then we get a second equation describing the movement of waves backwards in time, which is pretty peculiar but we're just upright apes so that's no reason to stop investigating.
The transactional interpretation of Quantum Mechanics shows that every event sends waves forwards and backwards in time, for example the emmission or absorbtion of radiation. However, we don't see these "waves from the future" since they stack up on top of each other and end up cancelling each other out. For example, an electron emits radiation and sends it forwards and backwards in time. Later on an electron absorbs this radiation and it too sends waves forwards and backwards in time. The forwards-in-time wave given out by the absorbtion exactly cancels with the forward-in-time wave given out by the emission, so at times after the absorbtion, the waves cancel to nothing. Likewise the backwards-in-time waves cancel for all times before the emmission, so there's nothing about an event which exists before it occurs (since the waves, when multiplied by their ocmplex conjugate, give probabilities. If the waves cancel to zero then the probability of anything to do with the wave existing at that point is zero). In the time between emmission and absorbtion, there is a wave travelling forwards in time and a wave travelling backwards in time, which turn out not to cancel, and we see one wave (the sum of the two) as we travel along in time. This is nice since we can swap the "i"s for "-i"s and get the same results, we'd just change the direction in time we're travelling in from "forwards" to "backwards", but like the +N and -N of Ed Daw's example, we've just made up those concepts as if they mean something. The reality is that there's no way of making such a distinction, so it becomes meaningless to try and find the values of "+N", "-N", "forwards" or "backwards". Just choose one and stick to it, like we normally choose "i" to be the positive root and "forward" to be the direction we perceive as our neurons interact thermodynamically.


















